FizzBuzzing

The Fizz Buzz program is a classic program used to test a programmer.

It’s very simple, you have to print numbers, but:

• if the number is a multiple of 3, you print Fizz
• if the number is a multiple of 5, you print Buzz
• if the number is a multiple of 3 and 5, you print FizzBuzz

In this article, we will see the classic version and a second version using a different logic.

If you want to test the javascript code, you can click below to add a special directive which will disable the optimization of the function.

Quick note here to say that in the code we will not use the string Fizz, Buzz and FizzBuzz but numbers.

Classic FizzBuzz in Javascript

const FIZZ = 1;
const BUZZ = 2;
const FIZZBUZZ = 3;

function fizzbuzz(n) {
    if (n % 3 == 0 && n % 5 == 0) {
        return FIZZBUZZ;
    } else if (n % 3 == 0) {
        return FIZZ;
    } else if (n % 5 == 0) {
        return BUZZ;
    }
    return n;
}

for (let i = 0; i < 1000000; i++) {
    console.log(fizzbuzz(i));
}

The twist: the algorithm is cycling!

If you look at the program and it’s output, you can see that the algorithm is cycling with a modulo of 15.

Why? because number divisible by 15 are divisible by 3 and 5 which is the FizzBuzz case.

# pip install z3-solver
from z3 import Solver, Int, Or, unsat

# Create a Z3 solver instance
solver = Solver()

# Create an integer variable
x = Int('x')

# Add the constraint that x is divisible by 15
solver.add(x % 15 == 0)

# Add the negation of the conclusion: x is not divisible by 3 or x is not divisible by 5
solver.add(Or(x % 3 != 0, x % 5 != 0))

# Check if the solver is satisfiable
if solver.check() == unsat:
    print("Every number divisible by 15 is also divisible by 3 and 5.")
else:
    print("There exists a number divisible by 15 that is not divisible by 3 or 5.")

Now let’s use that information to “optimize” the program: we don’t need to test every number! We can just cycle through the 15 cases.

FizzBuzz in Javascript using array

const FIZZ = 1;
const BUZZ = 2;
const FIZZBUZZ = 3;

const tab = [FIZZBUZZ, 0, 0, FIZZ, 0, BUZZ, FIZZ, 0, 0, FIZZ, BUZZ, 0, FIZZ, 0, 0];

function fizzbuzz(n) {
    const res = tab[n % 15];
    return res == 0 ? n : res;
}

for (let i = 0; i < 1000000; i++) {
    console.log(fizzbuzz(i));
}

Array are great, but we have some useless 0 values in it 😯!

FizzBuzz in Javascript using object

Here is an optimized version, using an object to remove useless 0 values.

const FIZZ = 1;
const BUZZ = 2;
const FIZZBUZZ = 3;

const tab = {
    0: FIZZBUZZ,
    3: FIZZ,
    5: BUZZ,
    6: FIZZ,
    9: FIZZ,
    10: BUZZ,
    12: FIZZ,
};

function fizzbuzz(n) {
    return tab[n % 15] ?? n;
}

for (let i = 0; i < 1000000; i++) {
    console.log(fizzbuzz(i));
}

Isn’t it beautiful? The fizzbuzz is only tab[n % 15] ?? n!

FizzBuzzing in C++

First, here is the main program, it uses a external fizzbuzz function.

We can also see that we are using a preprocessor directive to disable the output of the function.

#ifdef OUTPUT
#include <iostream>
#endif
constexpr int NUM = 10000000; // number of iterations

unsigned int fizzbuzz(unsigned int n);

int main()
{
    for (unsigned int i = 0; i < NUM; i++)
    {
#ifdef OUTPUT
        std::cout << fizzbuzz(i) << std::endl;
#else
        fizzbuzz(i);
#endif
    }
}

Second, for demonstration purpose we will use constants number to be replace words.

Classic FizzBuzz in C++

Just to remind you here is the classic fizzbuzz in C++:

constexpr int FIZZ = 1;
constexpr int BUZZ = 2;
constexpr int FIZZBUZZ = 3;

unsigned int fizzbuzz(unsigned int n)
{
    if (n % 3 == 0 && n % 5 == 0)
    {
        return FIZZBUZZ;
    }
    else if (n % 3 == 0)
    {
        return FIZZ;
    }
    else if (n % 5 == 0)
    {
        return BUZZ;
    }
    return n;
}

Array FizzBuzz in C++

constexpr int FIZZ = 1;
constexpr int BUZZ = 2;
constexpr int FIZZBUZZ = 3;

const int arr[15] = {FIZZBUZZ, 0, 0, FIZZ, 0, BUZZ, FIZZ, 0, 0, FIZZ, BUZZ, 0, FIZZ, 0, 0};

unsigned int fizzbuzz(unsigned int n)
{
    auto res = arr[n % 15];
    if (res == 0)
    {
        return n;
    }
    return res;
}

Benchmarking

Now let’s benchmark the different versions of the C++ programs. These benchmark were made using hyperfine.

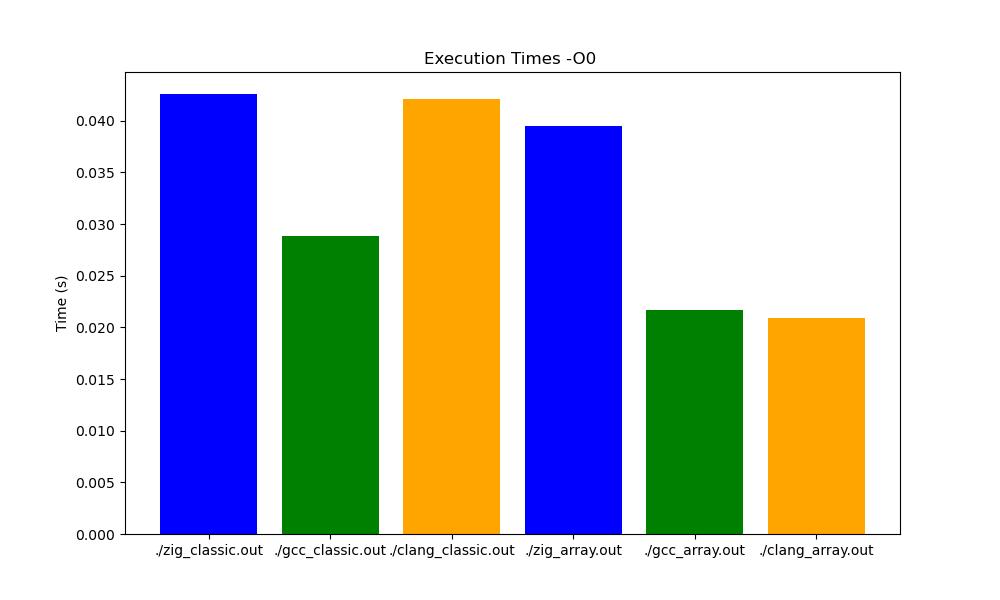
In this benchmark, we can see that results are quite the same with zig. However, we can see the difference between the classic version and the array version! We successfully optimized the program!

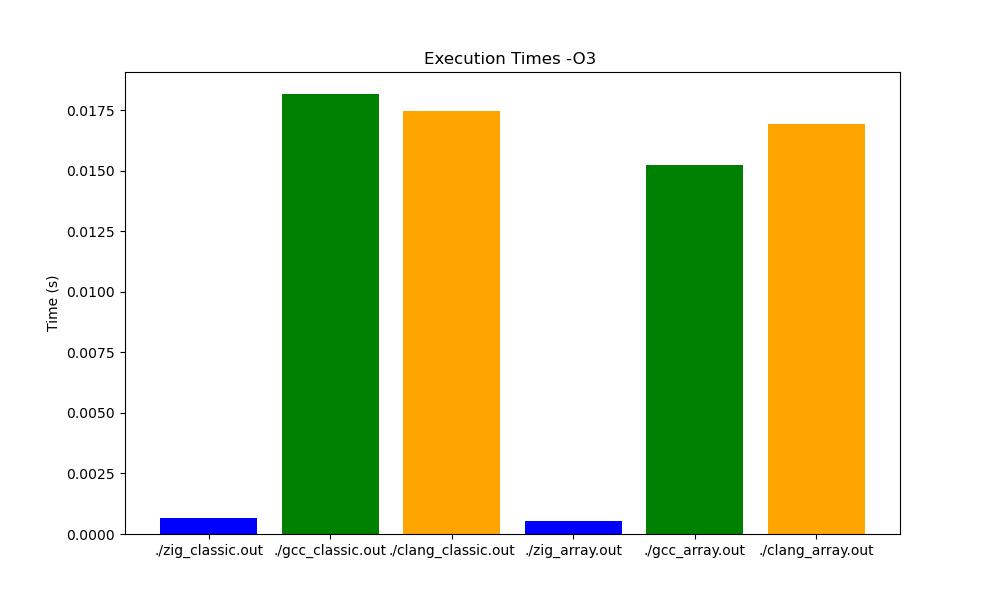
In this benchmark we can see that sadly, with optimization, results are quite the same! (I suppose zig this time decided to remove the whole program - quite an optimization).

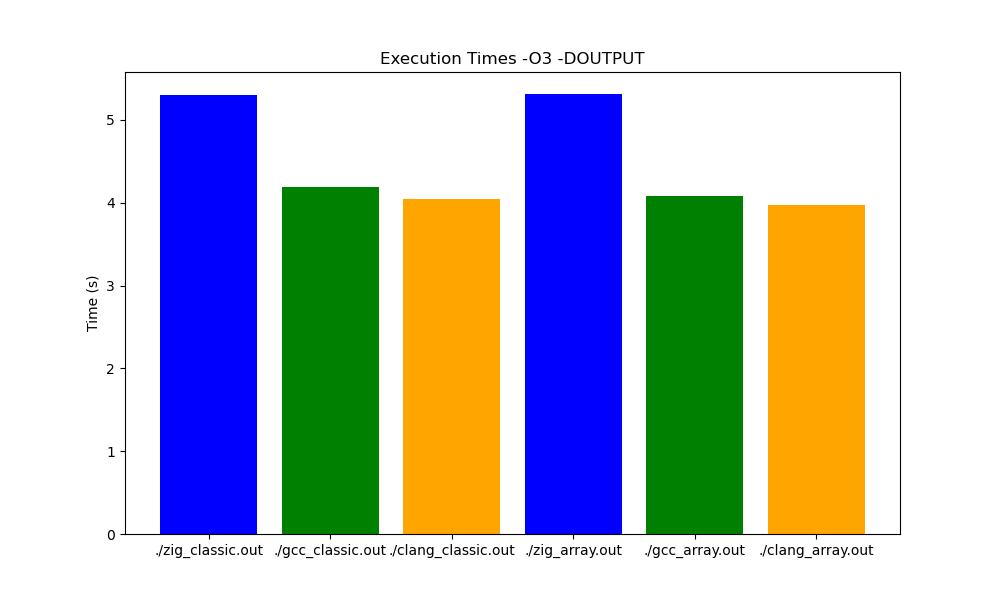
Finally, this benchmark show that with a real world program with an output, both version are equivalent because of the slowdown of writing to the output.

Conclusion

The focus of this article is on compiler optimizations. In the benchmark, we force the default optimization level of the compiler to -O0. But using optimization such as -O3, code will be optimized thanks to compilers and results are equivalents!

OPTIM=-O3
IO=-DOUTPUT
C=classic
A=array
CLASSIC=fizzbuzz_$(C).cpp
ARRAY=fizzbuzz_$(A).cpp
all: test


zig:
	zig c++ main.cpp $(CLASSIC) -o zig_$(C).out $(OPTIM) $(IO)
	zig c++ main.cpp $(ARRAY) -o zig_$(A).out $(OPTIM) $(IO)

gcc:
	g++ main.cpp $(CLASSIC) -o gcc_$(C).out $(OPTIM) $(IO)
	g++ main.cpp $(ARRAY) -o gcc_$(A).out $(OPTIM) $(IO)

clang:
	clang++ main.cpp $(CLASSIC) -o clang_$(C).out $(OPTIM) $(IO)
	clang++ main.cpp $(ARRAY) -o clang_$(A).out $(OPTIM) $(IO)


test: zig gcc clang
	hyperfine "./zig_$(C).out" "./gcc_$(C).out" "./clang_$(C).out" "./zig_$(A).out" "./gcc_$(A).out" "./clang_$(A).out" --export-json res$(OPTIM)$(IO).json
	$(MAKE) render

render:
	python graph.py res$(OPTIM)$(IO).json -o ../benchmark$(OPTIM)$(IO).jpg --title "Execution Times $(OPTIM) $(IO)"

data:
	$(MAKE) all OPTIM=-O0 IO=
	$(MAKE) all OPTIM=-O0 IO=-DOUTPUT
	$(MAKE) all OPTIM=-O3 IO=
	$(MAKE) all OPTIM=-O3 IO=-DOUTPUT

void fizzbuzz_full(int num_limit){
    for(int i = 0; i < num_limit;i++){
        fizzbuzz(i);
    }
}